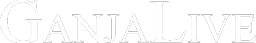От взаимодействия точечных масс к эффектам взаимодействия, когда одна из масс не является точечной.
По закону притяжения Ньютона две точные массы взаимодействуют с силой, прямо пропорциональной произведению точечных масс и обратно пропорциональной квадрату расстояния между ними.
А если одну из точечных масс разделить на две равных (для простоты задачи) половинки и эти половинки разнести на расстояние r друг от друга, оставив положение центра масс половинок в прежней точке (как до разделения. Как изменится сила притяжения между разнесенной массой и точечной, то есть оставленной как есть?
При чем, рассмотрим два случая:
Вариант А) Все три массы М и м/2 +м/2 остались лежать на одной линии.
Вариант Б) Половинки масс разнесли по линии перпендикулярной линии центров масс М и м

Далее Вариант А) решим графически:

На рисунке треугольники NOD и OKL равны по двум сторонам и углам между ними, значит ND равен KL. Следовательно PD заведомо больше KL.
То есть:
В гравитационном поле центрального тела выигрыш в работе при сближении точечной массы с центральным телом превышает затрату работы на удаление такой же массы на такое же расстояние.
Вариант Б)
При разносе масс по варианту Б) получается явный проигрыш в работе против сил поля, потому что обе массы удалились от центрального тела и суммарная сила притяжения упала.
Проводим окружность, массы m|2 лежат на касательной к окружности, то есть за окружностью.

Решение простейшей задачи с разносом массы одного из тел в гравитационном поле показало:
Если масса разносится по прямой от центр вращения(центр масс остается на месте), то гравитационное притяжение центральным телом при этом усиливается.
Если масса разносится по касательной к окружности вращения, то сила притяжения убывает.
Решение частного случая можно обобщить и экстраполировать для анализа поведения любого тела продолговатой формы в том числе и стержня на случай взаимодействия разнесенной массы с центральным телом. Отсюда вывод:
Тело с разнесенной массой имеет переменную силу притяжения центральным телом, зависящую от угла наклона линии разнесения масс к линии соединяющей центры масс.
То есть, тело с отклонениями от шаровой формы (продолговатое тело) не может двигаться по окружности вокруг центрального массивного тела и вращаться вокруг собственного центра масс одновременно, оно будет испытывать переменную силу притяжения и для компенсации этих вариаций вынуждено (центр масс продолговатого тела) совершать волнообразные колебания, то приближаясь к центральному телу, то удаляясь от него.
Данную работу следует считать приложением к работе «Пост ньютоновская механика». Просто здесь мы более строго доказали основные положения и выводы указанной работы.
Повторим только самый важный вывод:
Центр масс системы «Земля-Луна» совершает волнообразные движения по орбите, число волн равно числу оборотов системы вокруг центра масс (порядка двенадцати в год), то есть его движение не может быть ни идеальной окружность, ни идеальным эллипсом.
источник
По закону притяжения Ньютона две точные массы взаимодействуют с силой, прямо пропорциональной произведению точечных масс и обратно пропорциональной квадрату расстояния между ними.
А если одну из точечных масс разделить на две равных (для простоты задачи) половинки и эти половинки разнести на расстояние r друг от друга, оставив положение центра масс половинок в прежней точке (как до разделения. Как изменится сила притяжения между разнесенной массой и точечной, то есть оставленной как есть?
При чем, рассмотрим два случая:
Вариант А) Все три массы М и м/2 +м/2 остались лежать на одной линии.
Вариант Б) Половинки масс разнесли по линии перпендикулярной линии центров масс М и м

Далее Вариант А) решим графически:

На рисунке треугольники NOD и OKL равны по двум сторонам и углам между ними, значит ND равен KL. Следовательно PD заведомо больше KL.
То есть:
В гравитационном поле центрального тела выигрыш в работе при сближении точечной массы с центральным телом превышает затрату работы на удаление такой же массы на такое же расстояние.
Вариант Б)
При разносе масс по варианту Б) получается явный проигрыш в работе против сил поля, потому что обе массы удалились от центрального тела и суммарная сила притяжения упала.
Проводим окружность, массы m|2 лежат на касательной к окружности, то есть за окружностью.

Решение простейшей задачи с разносом массы одного из тел в гравитационном поле показало:
Если масса разносится по прямой от центр вращения(центр масс остается на месте), то гравитационное притяжение центральным телом при этом усиливается.
Если масса разносится по касательной к окружности вращения, то сила притяжения убывает.
Решение частного случая можно обобщить и экстраполировать для анализа поведения любого тела продолговатой формы в том числе и стержня на случай взаимодействия разнесенной массы с центральным телом. Отсюда вывод:
Тело с разнесенной массой имеет переменную силу притяжения центральным телом, зависящую от угла наклона линии разнесения масс к линии соединяющей центры масс.
То есть, тело с отклонениями от шаровой формы (продолговатое тело) не может двигаться по окружности вокруг центрального массивного тела и вращаться вокруг собственного центра масс одновременно, оно будет испытывать переменную силу притяжения и для компенсации этих вариаций вынуждено (центр масс продолговатого тела) совершать волнообразные колебания, то приближаясь к центральному телу, то удаляясь от него.
Данную работу следует считать приложением к работе «Пост ньютоновская механика». Просто здесь мы более строго доказали основные положения и выводы указанной работы.
Повторим только самый важный вывод:
Центр масс системы «Земля-Луна» совершает волнообразные движения по орбите, число волн равно числу оборотов системы вокруг центра масс (порядка двенадцати в год), то есть его движение не может быть ни идеальной окружность, ни идеальным эллипсом.
источник